Provenance Tracking in Python
1. The Code
You can find my code and paper on GitHub. Special thanks to Thomas Witte for advising me throughout the project.
2. Demonstration
Suppose we have some function in Python which we don't necessarily know the implementation of.
def blackbox(x): return 3 + (x * 7)
Using a wrapper provided from the library, you can call the function and calculate what input you have to give to the function in order to result in a desired output.
>>> from rosslt import Tracked >>> >>> expr = blackbox(Tracked(0.0)).get_expression() >>> param = expr.reverse()(42.0) >>> print(f"blackbox({param}) = {blackbox(param)}") blackbox(5.571428571428571) = 42.0
This works as long as the function is deterministic and the operations applied to the value does not change.
3. The Goal
We want to know what to input as x, so that the returned value would be 42.
Now obviously this can be done by looking at the function implementation code
and figuring out that you have to first subtract 3 from 42 and then divide the
result by 7 to get the solution. However, this can be done in an automated way.
4. Provenance Tree
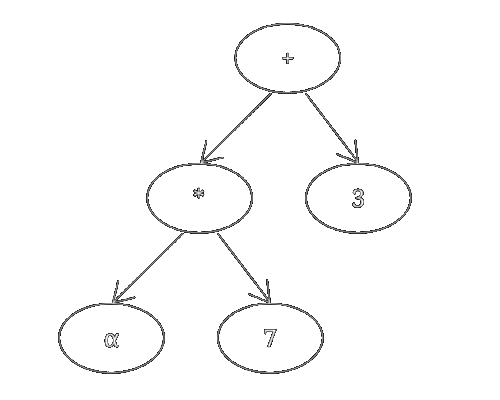
Figure 1: blackbox(x) in a tree for x = α
By creating a wrapper class overriding every operator, we can record all operations and store them in a tree structure. Python makes this easy, however there are quite a few operators to be implemented.
5. Tree Inversion
Provenance trees can be inverted relatively easy, though there are many cases to consider, especially because some operators are not commutative.
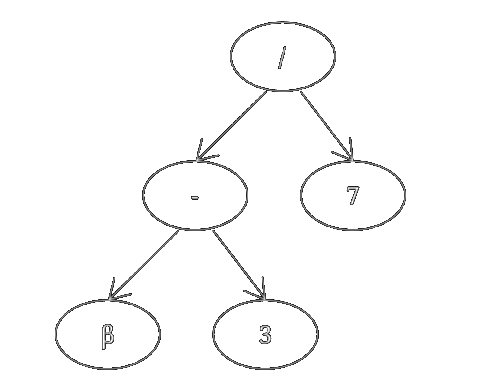
Figure 2: inverted provenance tree
6. Tree Evaluation
If we now evaluate the result we want of our blackbox function with the inverted provenance tree, we can calculate the required input in an automated fashion.
f(β) = (β - 3) / 7 f(42) = (42 - 3) / 7 = ~5.57
While this works for most cases, in some cases the evaluation of the provenance tree can have multiple solutions, such as when the value is multiplied by zero.
7. Optimizations
To make the library more efficient, there have been a few optimizations implemented.
7.1. Postfix Notation
The parameter count of all operations is fixed, which means the whole tree can be stored in postfix (RPN) notation within a linear list.
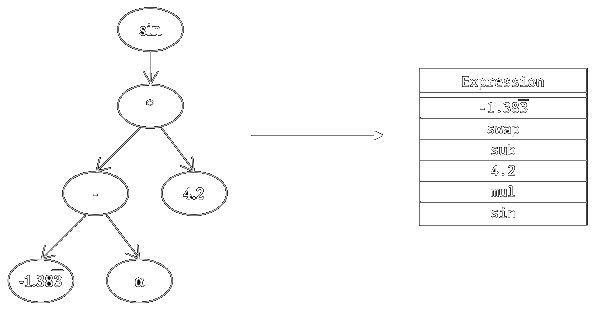
7.2. Serialization
By giving each operator a code and encoding the numbers, we can efficiently store the operations in a binary format.
| ID | Operator | Identifier |
|---|---|---|
| 0 | SWAP |
swap |
| 1 | ADD |
+ |
| 2 | SUB |
- |
| 3 | MUL_INT |
* |
| 4 | MUL |
* |
| 5 | DIV |
/ |
| 6 | DIV_FLOOR |
// |
| 7 | SIN |
sin |
| 8 | COS |
cos |
| 9 | ASIN |
asin |
| 10 | ACOS |
acos |
| 11 | POW |
pow |
| 12 | IPOW |
ipow |
To properly invert a floor division, we added an integer multiplication operator. There are also a few frequently basic trigonometric functions implemented.
| Code | Name | Size |
|---|---|---|
| 0x01 | INT32 | 4 bytes |
| 0x02 | INT64 | 8 bytes |
| 0x03 | DOUBLE | 8 bytes |
| 0x04 | COMPLEX | 16 bytes |
| 0x05 | STRING | variable |
Storing the values themselves works by defining a few data type codes. We can store both the operator and value codes in a single byte by using 4 bits each.
| Name | Data | Size |
|---|---|---|
| Expression | -1.3833333333333333;swap;-;4.2;*;sin | 36 bytes |
| Value Array | 222222222222F6BFCDCCCCCCCCCC1040 | 16 bytes |
| Code Array | 034042034447 | 6 bytes |

8. Location Tree

Figure 3: the concept
To properly support classes, we have to keep track of all the attributes, even when nested. The solution is to override the dot operator to return a temporary wrapper that keeps track of how nested it is and which path it has. Using a reference to the parent object it can record everything as necessary. I will not go into the details here, however.
9. Monitoring
For introspection and debugging purposes in ROS nodes, the library features a monitoring tool visualizing the provenance history as an expression string, with the ability to force specific values by notifying the value wrapper to override the source value with the automatically calculated required value. This works by evaluation the inverted provenance tree as shown above.
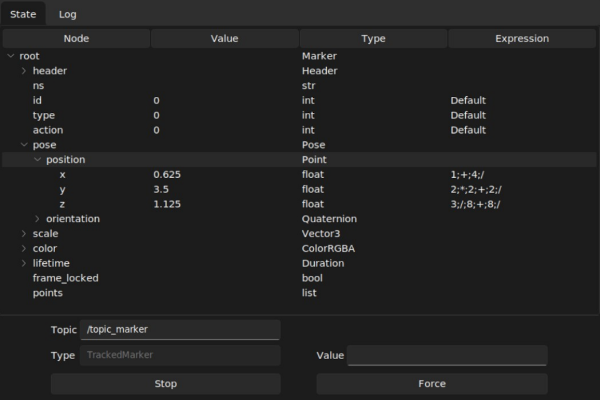
Figure 4: monitoring a ROS topic
10. Usage in ROS Nodes
10.1. Publisher
# create tracked instance marker_value = self.location(Marker()) # supports setting initial values outside instance creation marker_value.pose.position.x = 1.5 marker_value.pose.position.y = 2.5 marker_value.pose.position.z = 3.0 # apply calculation marker_value.pose.position.x += 1 marker_value.pose.position.y *= 2 marker_value.pose.position.z /= 3 # publish message self.publish(self.pub_marker, marker_value)
10.2. Subscriber
marker = Tracked.from_msg(msg) pos = marker.pose.position self.force_value(pos.x, pos.x + 1) self.force_value(pos.y, pos.y + 2) self.force_value(pos.z, pos.z + 3)
